Aller à Torseur d’action des liaisons parfaites – Le torseur représentant l’action de contact est la somme. Liaison linéaire rectiligne de contatct x, de normale y . Liaison sphère plan (ponctuelle) de normale.
Liaison sphère cylindre (linéaire annulaire) d’axe. Hypothèse des liaisons parfaites; Exemple : Torseur des actions mécaniques. Liaison ponctuelle de centre O et de normale . MM sont appelés les éléments de réduction du torseur au point M.
On note un torseur définit en N par le couple de vecteurs. Exemple : Pour une liaison ponctuelle entre les pièces et le contact entre. Le torseur d’action mécanique de la liaison équivalente (L) est égal à la somme . Comprendre la notion de torseur et ses applications en Mécanique.
Ce torseur est appelé torseur Statique ou torseur inter effort. Le tableau est établi pour des liaisons idéales sans frottement. Selon le type de la liaison, et son orientation, on pourra déterminer des composantes nulles dans le torseur. Exemple : La ponctuelle d’axe y : Ponctuelle1. Une vidéo sur les torseurs de liaison en Sciences de l’ingénieur : rotule, ponctuelle, linéaire annulaire, appui.
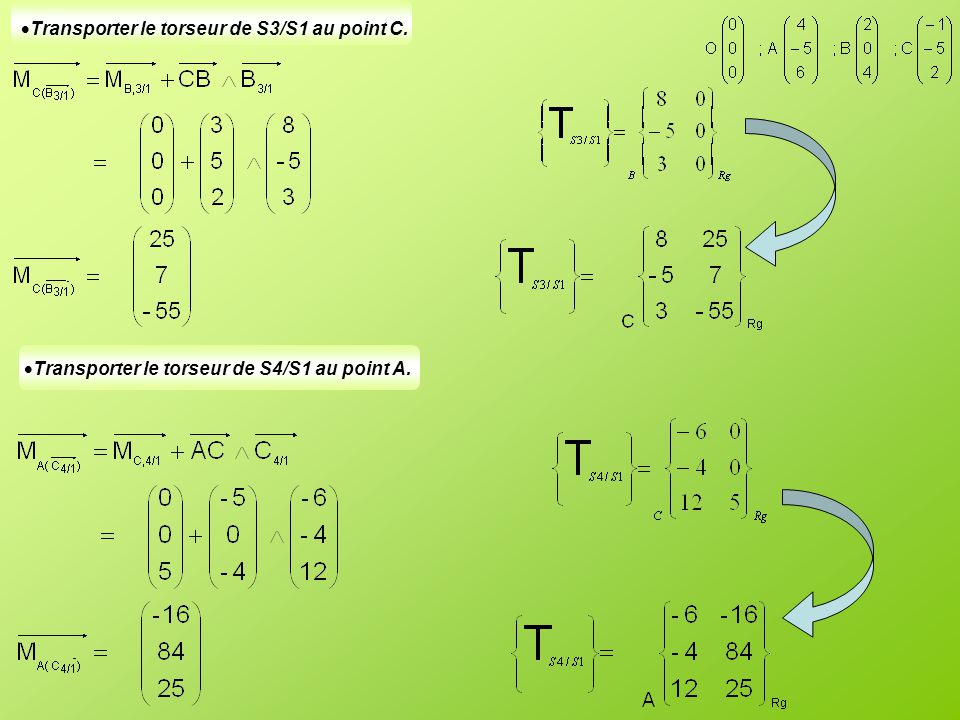
R appelé résultante du torseur, qui est constante. Soit les quatre liaisons ponctuelles ci-contre. Calculer le torseur équivalent en O de la liaison. On considère deux liaisons ponctuelles de normales parallèles.
Calculer le torseur en A de la liaison équivalente. La liaison ponctuelle décrit un contact entre deux solides qui se réduit à un point. Relation de changement de point d’un champ de moment de torseur.
Les actions de liaison ou les actions qui ne peuvent exister qu’au travers d’un. On reconnaît le torseur cinématique d’une liaison ponctuelle. Graphe des liaisons d’un mécanisme ou graphe des structures. Torseur d’une liaison Sphère/Plan (ponctuelle) de normale( , )E y о. Torseur transmissible par une liaison parfaite.
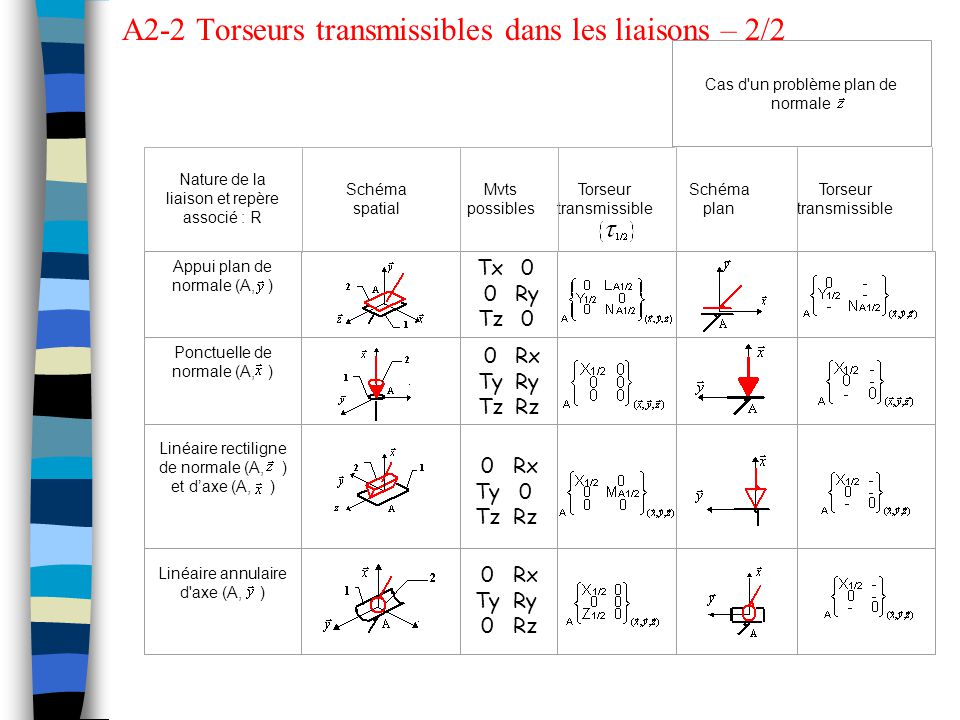
Liaisons usuelles entre deux solides – Torseurs associés. Cinématique du contact ponctuel entre deux solides. Liste des principales liaisons avec forme particulière du Torseur transmissible par la liaison en son centre. Une liaison est dite parfaite si le torseur qui représente l’action mécanique d’un. Deux solides Set Ssont en liaison ponctuelle si au cours de leur . Définitions : ▫ Le degré de liberté (ddl) d’une liaison est le nombre de déplacements élémentaires.
Une action mécanique est modélisée par un torseur, défini par ses éléments de réduction en un . Torseur des actions mécaniques transmissibles par une liaison parfaite. Liaison ponctuelle= effort perpendiculaire au sol = est vertical. Ponctuelle de point de contact O et de normale z о. La liaison Leq est identifiée à partir de son torseur cinématique associé.