Définition d’un Parallélogramme: Un parallélogramme est un quadrilatère convexe qui a ses côtés. Il existe des quadrilatères particuliers, dont les côtés, les angles et/ou les. Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.

Les diagonales d’un parallélogramme se coupent en leur milieu. Propriétés à utiliser pour prouver que la figure est un parallélogramme. Si un quadrilatère a ses côtés opposés parallèles deux à deux.

Définition : un losange est un quadrilatère dont les quatre côtés ont la même longueur.

Si un quadrilatère est un losange alors : ses diagonales sont . Définition : Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles deux à deux. Propriétés : – Si un quadrilatère est un parallélogramme . Propriétés générales et divers types de quadrilatères. S] Connaître et utiliser les propriétés réciproques pour démontrer qu’un quadrilatère est un parallélogramme.

Un quadrilatère est une figure à côtés. Propriété: La somme des angles intérieurs d’un quadrilatère est égale à 360°. En géométrie plane, un quadrilatère (parfois appelé tétrapleure ou tétragone) est un polygone.

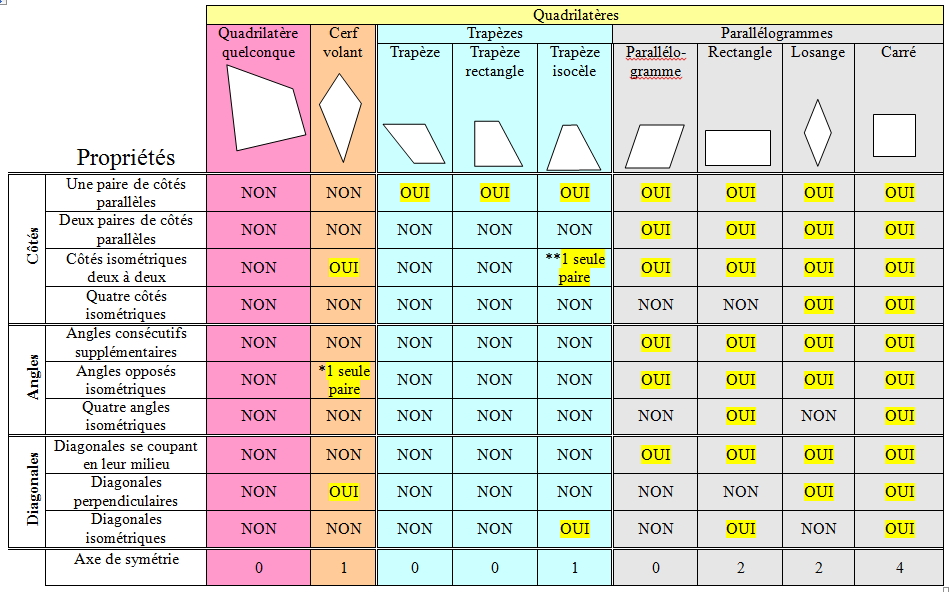
Ainsi, selon cette classification, le carré est le quadrilatère le plus riche en propriétés.

Il est aussi l’unique solution du problème isopérimétrique .