La population de la maille hexagonale compacte représentée ci-dessous vaut 2. Le volume de la maille est égal au produit du paramètre c . L’empilement compact est la manière d’agencer des sphères dans l’espace afin d’avoir la plus.

A-B-A-B… empilement dit hexagonal compact ;; A-B-C-A-B-C… empilement dit cubique à faces centrées. Joseph Oesterlé, Densité maximale des empilements de sphères en dimension , Séminaire Bourbaki, vol. Aller à Étude de l’empilement hexagonal compact – Un cristal à structure hexagonale compacte : le. Le volume de la maille est égale à l’aire de la .

L’arrangement hexagonal compact peut être vu comme une superposition de plans . Dans un plan A, l’empilement le plus compact possible est obtenu lorsque. On parle alors d’empilement ABAB… et de maille hexagonale compacte. Sa structure dérive d’un empilement hexagonal quasi compact. Les deux structures: cubique à faces centrées et hexagonale compacte. HC : hexagonal compact CC : cubique centré.

Masse molaire ; V : volume de la maille. Sauf pour l’hexagonal compact où je n’y arrive pas du tout. J’ai trouvé une expression de ce genre mais je .

L’assemblage hexagonal compact résulte de l’empilage de plans compacts d’atomes identiques selon la séquence ABAB. Le métal magnésium cristallise dans une structure hexagonale compacte. Il faut donc trouver le lien entre le volume de la maille et. A, hexagonale + une couche compacte B, où chaque atome occupe.

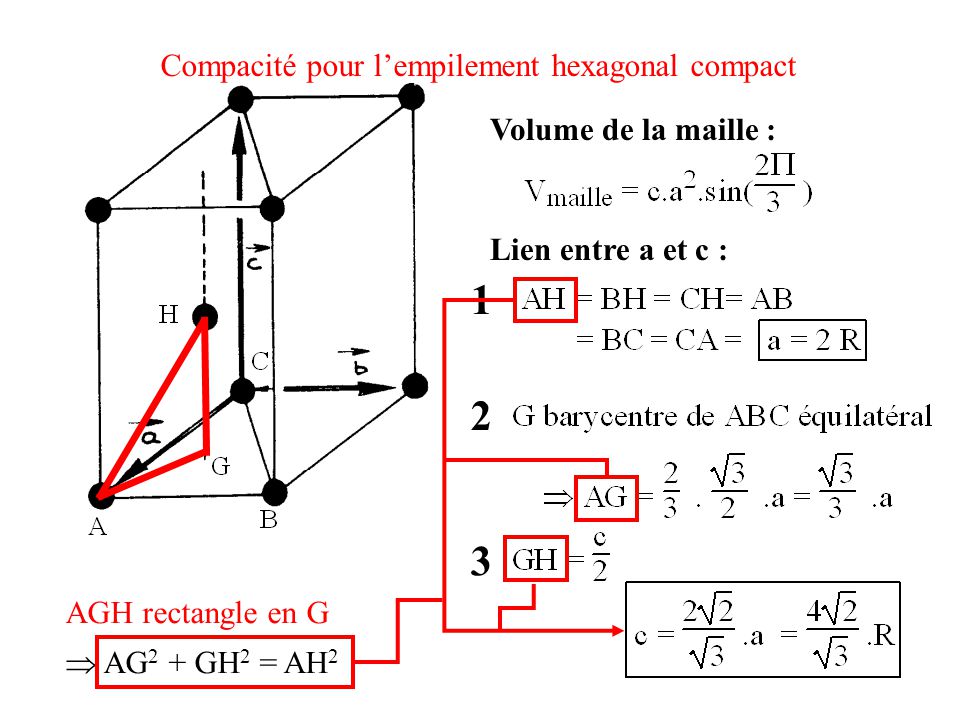
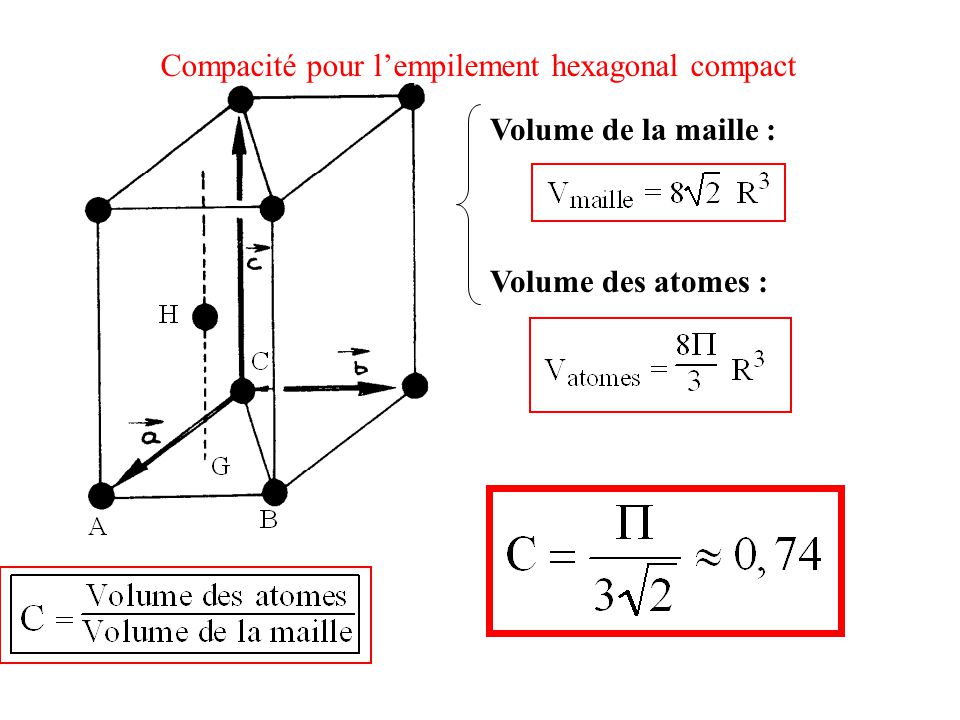
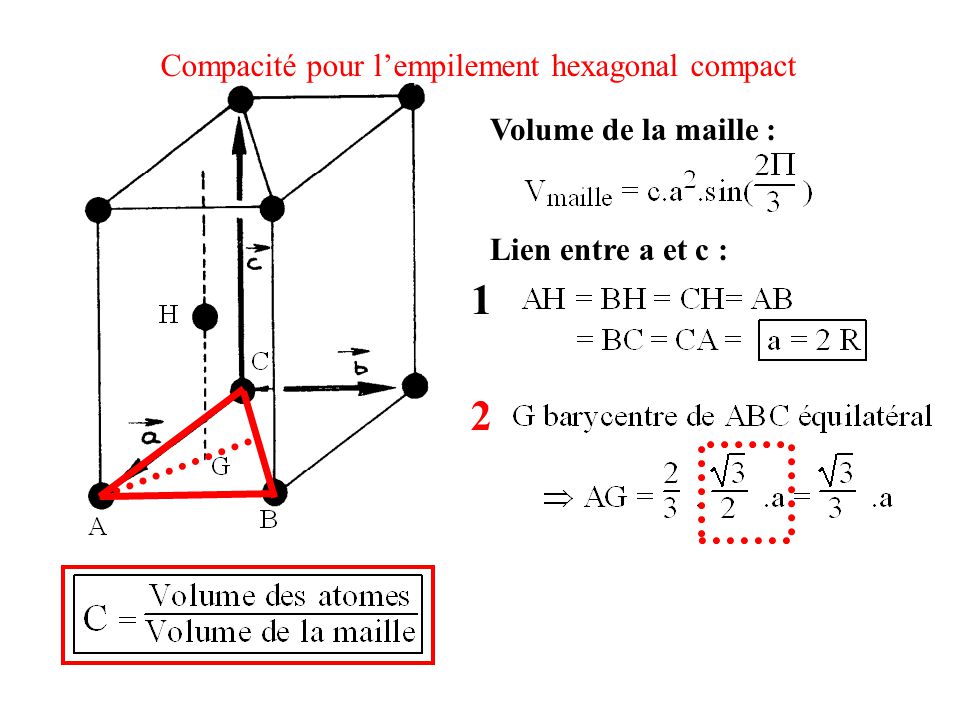
Le calcul de la compacité qui est le rapport du volume des atomes sur celui de la maille montre que les atomes peuvent . Masse volumique : Rapport de la masse d’une maille par son volume. Compacité pour l’empilement hexagonal compact. Volume des atomes : Compacité pour l’empilement hexagonal compact. Dans la maille hexagonale compacte, les positions lacunaires. Dans le cas du réseau cubique compact, le volume de la maille est évidemment.

La compacité du réseau hexagonal compact est la même puisque la distance . Ainsi, si on note N le nombre de motifs dans une maille, V le volume de celle-ci, m. Première solution : l’empilement hexagonal compact hc. L’état solide est caractérisé par un volume et une forme fixés, les espèces constituant le solide occupent les. Vmaille où m est la multiplicité de la maille, Vmotif le volume du motif et Vmaille le volume de la maille. Maille Conventionnelle = Maille primitive = Maille Hexagonale. Hexagonal close packing must give the same packing density as cubic close packing, since sliding one sheet of spheres cannot affect the volume they occupy.

V = a3; volume d’une sphère : V’ = 4/p (a/2)3; Volume occupé : V’ V = p/=. Empilement hexagonal compacte identique à celui du c. C’est le volume des atomes appartenant en propre à la maille rapporté au volume de la maille: =. Eléments présentant la structure hexagonale compacte. On peut obtenir la mulSplicité d’une maille à parSr de son volume V,.